I’ve just put my long paper “Time dispersion and quantum mechanics” up on the physics archive. If you are here, it is very possibly because you have at one point or another talked with me about some of the ideas in this paper and asked to see the paper when it was done. But if you just googled in, welcome!
The central question in the paper is “is time fuzzy? or is it flat?” Or in more technical language, “it time an observable? or is it a mere parameter?”
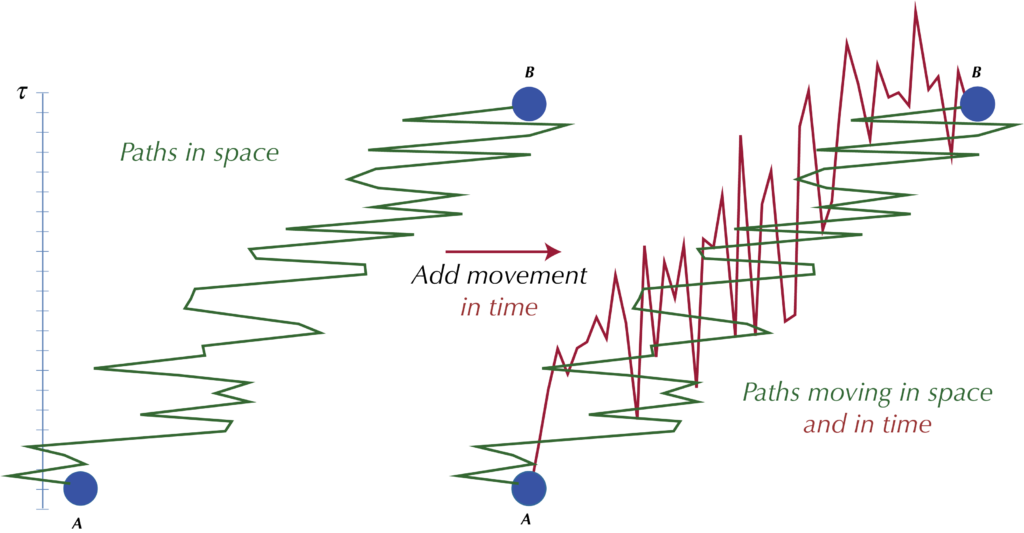
To recap, in relativity, time and space enter on a basis of formal equivalence. In special relativity, the time and space coordinates rotate into each other under Lorentz transformations. In general relativity, if you fall into a black hole time and the radial coordinate appear to change places on the way in. And in wormholes and other exotic solutions to general relativity, time can even curve back on itself.
For all its temporal shenanigans, in relativity everything has a definite position in time and in space. But in quantum mechanics, the three space dimensions are fuzzy. You can never tell where you are exactly along the x or y or z positions. And as you try to narrow the uncertainty in say the x dimension, you inevitably (“Heisenberg uncertainty principle”) find the corresponding momentum increasing in direct proportion. The more finely you confine the fly, the fiercer it buzzes to escape. But if it were not for this effect, the atoms that make us — and therefore we ourselves in turn — could not exist (more in the paper on this).
So in quantum mechanics space is complex, but time is boring. It is well-defined, crisp, moves forward at the traditional second per second rate. It is like the butler Jeeves at a party at Bertie Wooster’s Drone’s Club: imperturbable, stately, observing all, participating in nothing.
Given that quantum mechanics and relativity are the two best theories of physics we have, this curious difference about time is at a minimum, how would Jeeves put it to Bertie?, “most disconcerting sir”.
Till recently this has been a mere cocktail party problem: you may argue on one side, you may argue on the other, but it is more an issue for the philosophers in the philosophy department than for the experimenters in the physics department.
But about two years ago, a team led by Ossiander managed to make some experimental measurements of times less than a single attosecond. As one attosecond is to a second as a second is to the age of the universe, this is a number small beyond small.
But more critically for this discussion, this is roughly about how fuzzy time would be if time were fuzzy. A reasonable first estimate of the width of an atom in time is the time it would take light to cross the atom — about an attosecond.
And this means that we can — for the first time — put to experimental test the question: is time fuzzy or flat? is time an observable or a parameter?
To give the experimenters well-defined predictions is a non-trivial problem. But it’s doable. If we have a circle we can make some shrewd estimates about the height of the corresponding sphere. If we have an atomic wave function with well-defined extensions in the three space dimensions, we can make some very reasonable estimates about its extent in time as well.
The two chief effects are non-locality in time as an essential aspect of every wave function and the complete equivalence of the Heisenberg uncertainty principle for time/energy to the Heisenberg uncertainty principle for space/momentum.
In particular, if we send a particle through a very very fast camera shutter, the uncertainty in time is given by the time the camera shutter is open.
In standard quantum mechanics, the particle will be clipped in time. Time-of-arrival measurements at a detector will show correspondingly less dispersion.
But if time is fuzzy, then the uncertainty principle kicks in. The wave function will be diffracted by the camera shutter. If the uncertainty in time is small, the uncertainty in energy will be large, the particle will spread out in time, and time-of-arrival measurements will show much greater dispersion.
Time a parameter — beam narrower in time. Time an observable — beam much wider in time.
And if we are careful we can get estimates of the size of the effect in a way which is not just testable but falsifiable. If the experiments do not show the predicted effects at the predicted scale, then time is flat.
Of course, all this takes a bit of working out. Hence the long paper.
There was a lot to cover: how to do calculations in time on the same basis as in space, how to define the rules for detection, how to extend the work from single particles to field theory, and so on.
The requirements were:
- Manifest covariance between time and space at every step,
- Complete consistency with established experimental and observational results,
- And — for the extension to field theory — equivalence of the free propagator for both Schrödinger equation and Feynman diagrams.
I’ve been helped by many people along the way, especially at the Feynman Festivals in Baltimore & Olomouc/2009; at some conferences hosted by QUIST and DARPA; at The Clock and the Quantum/2008 conference at the Perimeter Institute; at the Quantum Time/2014 conference Pittsburgh; at Time and Quantum Gravity/2015 in San Diego; and most recently at the Institute for Relativistic Dynamics (IARD) conference this year in Yucatan. An earlier version of this paper was presented as a talk at this last conference & feedback from the participants was critical in helping to bring the ideas to final form.
Many thanks!
The paper has been submitted to the IOP Conference Proceedings series. The copy on the archive is formatted per the IOP requirements so is formatted for A4 paper, and with no running heads or feet. I have it formatted for US Letter here.