Why quantum time?
Why quantum time?
A few years ago I was looking for an interpretation/formalism for quantum mechanics which would be manifestly symmetric between time and space. The first question I had was:
Is time already quantized?
Is time treated using the same quantum rules as space is? can quantum mechanics be written in a way which is manifestly covariant?
(I do not mean, does time come in small quanta?, say of order the Planck time. It might perfectly well do so, but this would be independent of the question I am asking here.)
I looked at John Cramer’s Transactional Interpretation but while this is promising (the Transactional Interpretation has no preferred direction in time, sees all time as laid out at once just as space is) Cramer states, explicitly, that it reduces in all cases to the usual quantum mechanics:
It should be emphasized that the [Transactional Interpretation] is an interpretation of the existing formalism of quantum mechanics rather than a new theory or revision of the quantum mechanical formalism. As such, it makes no predictions which differ from those of conventional quantum mechanics.
And the problem here is that standard quantum mechanics for single particles treats – or seems to treat – time and space very differently. In standard quantum mechanics:
1. Time is a parameter, not an operator. See for instance von Neumann’s statement:
First of all we must admit that this objection… points to an essential weakness which is, in fact, the chief weakness of quantum mechanics: its non-relativistic character, which distinguishes the time t from the three space coordinates x, y, z, and presupposes an objective simultaneity concept. In fact, while all other quantities (especially those x,y,z closely connected with t by the Lorentz transformation) are represented by operators, there corresponds to the time an ordinary number-parameter t, just as in classical mechanics.
2. The time/energy uncertainty relation appears to be on a very different basis that the space/momentum uncertainty relations. See for instance Jonathan Oppenheim’s thesis Quantum Time or Paul Busch’s “The time-energy uncertainty relation” in Muga et al’s collection Time in Quantum Mechanics (Lecture Notes in Physics) (v. 1).
Of course we do not really expect to see manifest covariance of time and space in the non-relativistic Schrödinger equation. And when we look at the fully relativistic case, we see that the Feynman path integral approach to quantum electrodynamics seems fully symmetric between time and space. However, Steven Weinberg notes:
although the path-integral formalism provides us with manifestly Lorentz-invariant rules, it does not make clear why the S-matrix calculated in this way is unitary. As far as I know, the only way to show that the path-integral formalism yields a unitary S-matrix is to use it to reconstruct the canonical formalism, in which unitarity is obvious.
And in the canonical formalism time and space are manifestly not on an equal footing.
So far as I know, there is no treatment of quantum mechanics which both:
- Treats time and space in a manifestly covariant way
- Is manifestly unitary, i.e. where the probability of a result is always one.
Why look for quantum time?
- It is a logically necessary alternative: the only way we can be sure we shouldn’t quantize along the time dimension is to try to do so — and find we can’t.
- Quantum time is an experiment factory: for most foundational experiments in quantum mechanics we will get a test of quantum time if we flip time and a space dimension. The single and double slit experiments have single and double slit in time equivalents, the Aharonov-Bohm experiment has an Aharonov-Bohm in time equivalent (actually at least two), and so on. As there are several hundred foundational experiments in quantum mechanics (see for instance, Gennaro Auletta’s Foundations and Interpretation of Quantum Mechanics: In the Light of a Critical-Historical Analysis of the Problems and of a Synthesis of the Results) there is no shortage of tests possible.
- Quantum time provides a potentially useful perspective on standard quantum mechanics.
- Quantum time provides a natural starting point for investigation in other areas where time is important, i.e. quantum gravity, quantum computing, and quantum communication.
- Quantum time is an inherently interesting idea; fuzzy time is fun.
How to define the rules for quantum time?
The most obvious line of attack is to take some nearby formalism, something nearly symmetric between time and space, and walk it over till it gets the job done. We’ll do this using path integrals, for the single particle case.
We start by defining laboratory time as what is measured by clocks, laser beams, and grad students. We call this τ. Then for any fixed value of the laboratory time, we generalize the wave function of a particle to extend in time as well as space:
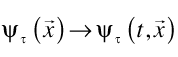 The latin t is the quantum time. At each instant of laboratory time, the wave function of the particle has an extension in quantum time t just as it does in space. Given special relativity, it is difficult to see how a fully covariant wave function could not have an extension in time. The wave function, indexed by τ, is the experimenter’s best estimate of where the particle is in time and space as of each instant in laboratory time.
The latin t is the quantum time. At each instant of laboratory time, the wave function of the particle has an extension in quantum time t just as it does in space. Given special relativity, it is difficult to see how a fully covariant wave function could not have an extension in time. The wave function, indexed by τ, is the experimenter’s best estimate of where the particle is in time and space as of each instant in laboratory time.
Think of τ as the number of clock ticks: at tick 1 there is a wave function, at tick 2 a slightly different one, eventually at tick# [insert large number here] we register a click at a detector. If the wave function is well-spread out in quantum time, we’ll see clicks earlier and later than standard quantum theory would predict. If it is narrow in quantum time, the results will be indistinguishable from the usual. Basically, the main prediction of quantum time is that everything is a bit more fuzzy in time than you would have thought: the separation of past and future not so clean and well-defined as one might have expected.
To actually compute what the wave function looks like at each clock tick we use path integrals, generalizing the usual paths in three-space to include paths that jump about in time as well. We have to make sure that the most complete symmetry is maintained between t and the space dimensions, that being the defining condition of quantum time.
Once we have our path integrals defined in a manifestly covariant way (and convergent and normalized), we use their short time behavior to derive the corresponding Schrödinger equation:
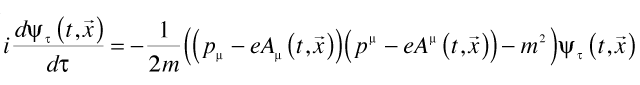
This is the defining equation of quantum time. The four-vector p is composed of the energy and the three momentum; the four-vector potential A is composed of the electric potential Φ and the usual three vector vector potential. Covariance is manifest, provided the laboratory time τ is a scalar.
To solve this four-dimensional Schrödinger equation, we have to make some assumptions about the initial wave function, turn the crank, perhaps invoke an approximation or two, see what comes out.
In general, we will need a two step procedure to do a test of quantum time: first send a beam thru a chopper to give it a known size in time, then use it in a double slit or what-have-you experiment.
What questions do we have to answer?
With the basic strategy laid it, the problem becomes one of executing against it. This is largely a matter of dealing with a series of questions & finding some reasonable response to each. (We aren’t going for perfection here; we are going for falsifiable.)
- How do we define and do the path integrals?
- How do we describe the wave functions?
- How do we define the paths?
- What Lagrangian should we use?
- How do we ensure the integrals converge?
- How do we normalize the integrals?
- How do we derive the four-dimensional Schrödinger equation?
- How do we demonstrate unitarity?
- What gauge transformations are possible?
- How do we prove we have done the maths correctly?
- How do we define the laboratory time so that it is a scalar?
- Do we recover the classical equations of motion in the classical limit?
- Do we recover the usual three-dimensional Schrödinger equation in the non-relativistic case?
- How do we go from the four to the three dimensional Schrödinger equation in general?
- What corrections do we see to the three-dimensional Schrödinger equation?
- Are they so large we would have seen them even if we weren’t looking for them?
- Do we recover the Bohr orbital condition for bound states?
- How do we define the results of an experiment in terms of detector clicks per second of laboratory time?
- What experiments can we do?
I argue in the full paper that we can give reasonable answers to all of these questions. I’d give them here but then I would be putting the entire paper into this post. I give an overview of the paper in an earlier post.
I don’t try to show that the resulting quantum time is unique. I do show that it is the simplest quantum time which meets the requirements:
- Well-defined.
- Manifestly symmetric between time and space.
- Consistent with known experimental results.
- Testable.
- Reasonably simple.
Some of the intermediate results in the full paper may be of interest in their own right. For instance to make sure the initial wave functions are well-defined and to ensure the path integrals converge, I use Morlet wavelet decomposition. Morlet wavelet decomposition lets us write an arbitrary wave function as a sum of Gaussian wave packets. Once this is done, we get convergence of the path integrals – without using magic convergence factors or Wick rotation.
Is quantum time true?
That I don’t know. But it is testable. Possible results are:
- Time is not fuzzy.
- Time is fuzzy, but not in quite the expected way. Perhaps time is fuzzier in some frames than others. (This might provide a way to locate a “preferred frame for the universe”, possibly its center of mass frame.)
- Time and space are fuzzy in the same way.
- None of the above.
Even the first result would be interesting. How could we have all three of: time not fuzzy, space fuzzy, and quantum mechanics consistent with special relativity? Something would have to give; the failure would be the opportunity.
And if the first result is interesting, the remaining results are increasingly more interesting. I would be surprised if quantum time turned out to be true exactly as given, but I think it is very likely – from special relativistic considerations alone – that there are some quantum effects along the time dimension. With a well-defined theory as a point of reference, we can reasonably hope that an experimental program will resolve the question.