Time dispersion in Quantum Electrodynamics
I gave a talk in June at the IARD 2022 conference in Prague on “Time dispersion in Quantum Electrodynamics”. I can’t improve on the abstract so give it here:
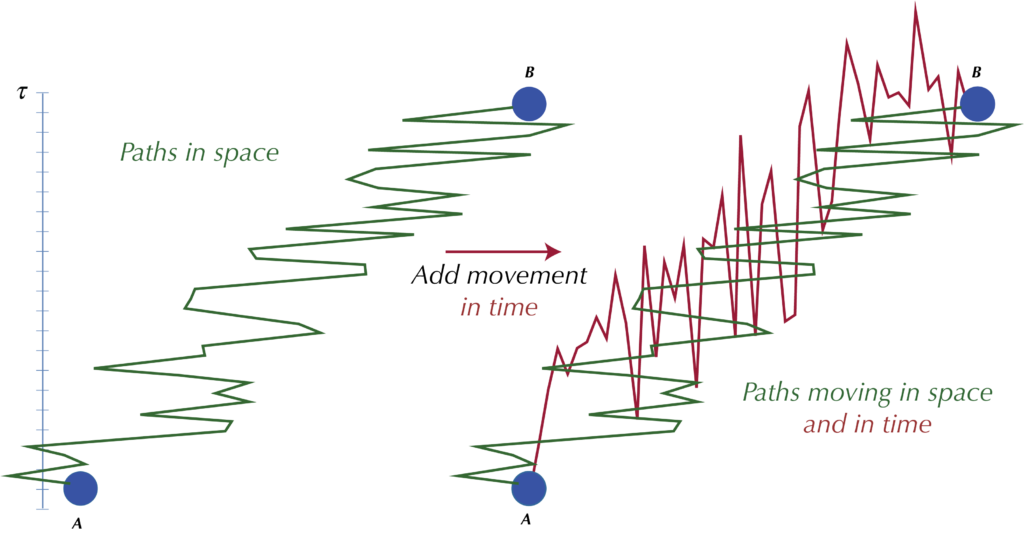
Quantum electrodynamics (QED) is often formulated in a way that appears fully relativistic. However since QED treats the three space dimensions as observables but time as a classical parameter, it is only partially relativistic. For instance, in the path integral formulation, the sum over paths includes paths that vary in space but not paths that vary in time. We apply covariance to extend QED to include time on the same basis as space. This implies dispersion in time, entanglement in time, full equivalence of the Heisenberg uncertainty principle (HUP) in time to the HUP in space, and so on. In the long time limit we recover standard QED. Further, entanglement in time has the welcome side effect of eliminating the ultraviolet divergences. We should see the effects at scales of attoseconds. With recent developments in attosecond physics and in quantum computing, these effects should now be visible. The results are therefore falsifiable. Since the promotion of time to an operator is done by a straightforward application of agreed and tested principles of quantum mechanics and relativity, falsification will have implications for those principles. Confirmation will have implications for attosecond physics, quantum computing and communications, and quantum gravity.
I’ve written the talk up as a paper and submitted to the IARD’s Conference Proceedings, where it is undergoing peer review. I’ve also submitted it to the physics archive, so Time dispersion in quantum electrodynamics is generally available.
It’s a long paper, 95 pages, but in defense of that it is a large subject. A quick check on bookfinder.com showed over 1000 textbooks on QED — and at 3 centimeters a book (based on my personal library) the literature — just the textbooks — runs over 30 meters! The problem I had was how to extend QED in time without breaking it. QED has, after all, been confirmed to extraordinary precision: is there room for time within QED?
The basic trick was to write the extension as the standard theory times a “time correction”. So if the time correction is small enough, we won’t have seen it by accident. Since the time corrections will normally be about an attosecond in size (an attosecond is to a second as a second is to the age of the universe), that’s not hard to show.
The other trick is to show that there are cases where we could see the effects of these “time corrections”. Since we can now see stuff at the attosecond level — provided we know where to look — that’s OK as well.
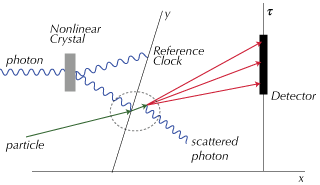
The illustration at the top of this post is a proposed test of the Heisenberg Uncertainty Principle in time, which is particularly nice because in this case the effect can be made — in principle at least — as large as we like. But there are lots of other possibilities:
“With respect to the falsifiability of TQM [time correction to QED], the small size of the basic effect may be compensated for by the large number of experimental possibilities. If quantum mechanics should in fact be extended in the time direction then essentially any time dependent apparatus with time dependent detectors may provide a possible line of attack. By hypothesis, all quantum mechanical phenomena seen in space – interference, diffraction, uncertainty, entanglement, tunneling, … – apply in time as they do in space.
But what are the odds of this being true? I give five reasons (explained in detail in the text):
- We have a version of QED which is manifestly covariant, treating all four dimensions equally. Simply being able to do this is interesting.
- We have a clear explanation of why time normally appears asymmetric at the level of the observer (due to statistical effects at the scale of Avogadro’s number) while still at the particle level being completely symmetric.
- We have a treatment which goes smoothly from the single to the multiple particle cases.
- We do not see the ultra-violet divergences. We still have to normalize the loops, but we no longer have to regularize them: that drops out of the formalism.
- And we have Gell-Mann’s principle: what is not forbidden is compulsory. If there is not a conservation principle or symmetry rule forbidding dispersion in time, it would be surprising not to see dispersion in time.
And if QED really should extend in time, there may be some significant uses:
High speed chemical and biological interactions, i.e. attosecond scale, should show effects of time dispersion. For instance, if molecules can sense into the future, it may affect their ability to find optimal configurations. There are potential applications for quantum communication and quantum computing. With TQM we have an additional channel to use for calculation/communication but also an additional channel to act as a source of decoherence.The implications for quantum gravity are particularly interesting: with manifest covariance, elimination of the ultra-violet divergences, some recent work by Horwitz, and earlier work by Verlinde, we appear to have all the pieces needed to construct a complete, covariant, and convergent theory of quantum gravity. Leaving the question of the odds of this being correct to one side, we note that recent advances in technique mean such a theory has a reasonable chance of being falsifiable as well.
My personal favorite effect is the possiblity of tunneling in time. The posited symmetry between time and space forces this, but does it mean?