Relativistic Morlet Wavelets

Wavelets are like musical notes: they are wave forms limited in both time and frequency. What makes them particularly useful is that any reasonable wave function may be written as a sum over them.

Usually we think of music in terms of pure tones, in terms of its Fourier components. But pure tones can be a bit too pure. For one thing, if a tone is to be completely pure it has to last forever, not a characteristic associated with practical questions. Wavelets are impure tones, and therefore a better match to the real world.

Wavelets have found applications in an abecedary of fields : in acoustics, astronomy, atomic physics, breast cancer diagnosis, computer graphics, finance, fingerprint analysis, medical imaging, materials science, movies (hard to destroy the world in a really satisfying way without using wavelets for the graphics), quantum mechanics, weather studies, and the analysis of zebra stripe patterns.

Wavelets are produced by starting with a mother wavelet, squeezing or stretching it and shifting it left or right. As they used to say on the Outer Limits: “we control the horizontal, we control the vertical”.

As with life, so with wavelets: correct choice of your mother is the essential first step. Two of the most popular choices for wavelet mother are the Mexican Hat function — which looks like a Mexican hat — and the Morlet wavelet, which is a Gaussian and looks like a bell-shaped curve times a sine wave:

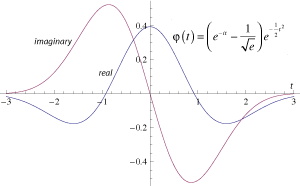
Mother Morlet wavelet

The mother Morlet wavelet is given by the formula:

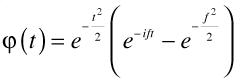
Mother Morlet wavelet

where the f is a reference frequency and the second term is there to make sure that the average value of the mother wavelet is zero: wavelets have to be purely oscillatory:  they are all AC, no DC.

After shifting and squeezing and stretching we get the typical wavelet:

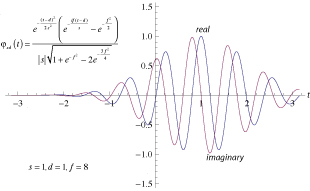
Typical Morlet wavelet

with the formula:

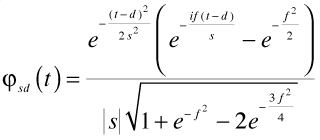
Morlet wavelet

Pay no attention to the small factor in the denominator; it is only there for the normalization.

Mostly wavelets are used for practical applications, but it seems Morlet wavelets may have some interesting applications in dealing with the fundamental questions of quantum mechanics. I ran into this while working on my dissertation: it turned out there was no way I could get the path integrals I was using to work without using wavelets to describe my wave functions. Because wavelets are smooth and localized they cause nearby integrals to converge & calculations to behave much better than they might otherwise want to.

There is another question Morlet wavelets may be a big help with. If you have hung around quantum mechanics long enough, you will have heard them talk about the “collapse of the wave function”. This is the mysterious transition from the quantum mechanical domain to ours. At the quantum level, everything is uncertain and wavy. At ours, things are definite and have hard-edges. How do we get from the level of the atom to the level of us?

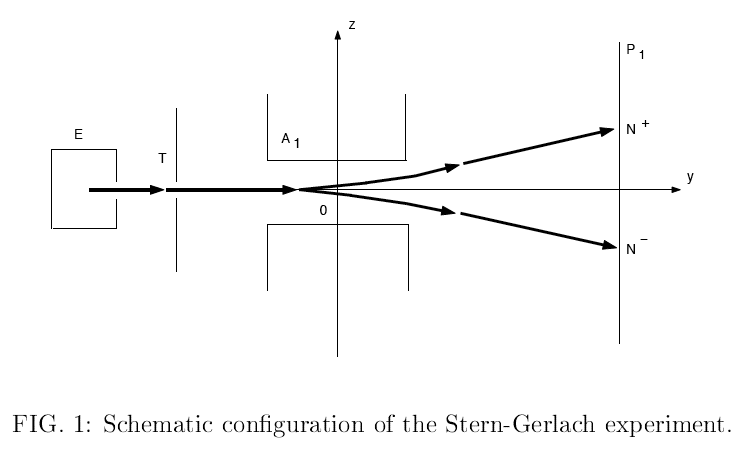
For instance, take the Stern-Gerlach experiment. In this classic quantum mechanics experiment:

a beam of silver atoms is sent thru a magnetic field. Silver atoms have spin and their spin can point in any direction.  The atom’s spin interacts with the magnet’s magnetic field, so if the atom has one spin, it gets kicked up, if the opposite spin, it gets kicked down.  The problem is “what about all the spins in the middle”? It turns out that every atom is either kicked up or kicked down, there is no middle (no comparisons to any dysfunctional political process is being made).

The resolution in the Copenhagen interpretation of quantum mechanics is that the silver atom’s wave function “collapses” into either an up or a down state. This is frankly more a label than an explanation: is the collapse real? if it is, when did it happen? and how did the atom “know” to go up or down as opposed to left or right?

A few years ago Gondran and Gondran posted on the web a very interesting paper where they were able to dispense with the mysterious collapse by doing the analysis a bit more realistically. They assume the atom starts out not with one pure spin but with a Gaussian distribution of spins (like a fuzzy sphere, where the spins point in all directions) and then let the Schödinger equation guide the particle thru the magnetic beam.

It turns out that the atom’s wavefunction interferes with itself to choose either up or down. All the other paths show destructive interference; only these two routes show coherent interference. The magnetic field acts like a kind of bifocal lens.

The key trick was the assumption of an initial Gaussian distribution; a wavelet. An analysis in terms of pure spins forces you to invoke the collapse of the wave function; an analysis in terms of wavelets — a Gaussian distribution is a Morlet wavelet — lets you get rid of the magic. Which is of course what science is about.

In any case, when I was working with Morlet wavelets I realized I really needed to have Morlet wavelets that worked not just in one dimension but in all four: time and the three space. I bypassed the problem in the paper itself (whenever you encounter thin ice, wave your hands energetically to generate lift enough to let you glide over the thin bit) but the problem bothered me.

To put the question to rest, I’ve written a paper, Relativistic Morlet Wavelets, to generalize Morlet wavelets to four dimensions.  It is not particularly tricky to do this, but I didn’t see it done anywhere in the literature. As I argue in the paper, four dimensional Morlet wavelets may help in solving some of the problems with the relativistic theory of electrons, quantum electrodynamics (QED), just as one dimensional Morlet wavelets can help with some of the problems in non-relativistic quantum mechanics (the Schödinger equation and its friends).

Comments, links, and suggestions much appreciated!

John