Overview
In relativity time and space are treated symmetrically but in quantum mechanics the treatment of time is very different: in quantum mechanics time enters as a parameter, not an observable.
In my dissertation, I bridge this gap from the quantum mechanics side by quantizing time using the same rules as for space and then seeing what happens.
To start, we define the laboratory time as what is measured by clocks, lasers, & grad students. At any instant in laboratory time τ we have the wave function of a particle in space:
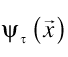
We posit this wave function extends into the time dimension as well:
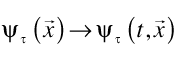
Given the wave function at one instant in time, we need to figure the wave function at the next instant, we need dynamics. To do this we will use Feynman’s path integrals.
Path integrals are like good beer: all you need are a few simple ingredients and a bit of time. The few simple ingredients are a starting wave function, some paths and a Lagrangian.
For the starting wave function I didn’t want to use plane waves or δ functions as they are not normalized & can therefore create artifacts (time is confusing enough in its own right). The usual Gaussian wave packets are more physically reasonable, but not general. However we can use Morlet wavelets, which are both physically reasonable and completely general. Morlet wavelets are defined as:
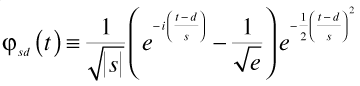
where s and d are the scale and the displacement. Typical wavelet:
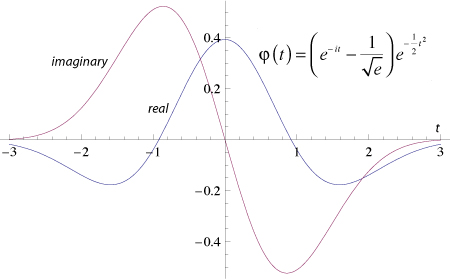
- Real and imaginary parts of a Morlet wavelet
Any square-integrable function may be decomposed in terms of Morlet wavelets:
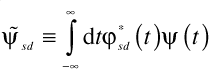
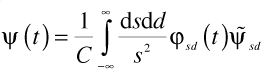
As Morlet wavelets are sums of Gaussians they are easy to work with.
For the paths we generalize the usual paths in the three space dimensions to include paths in time as well:
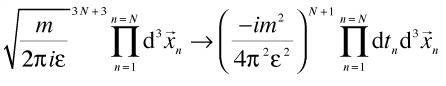
For the Lagrangian we use:
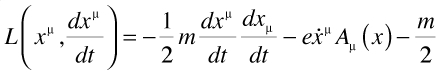
This Lagrangian gives the correct classical equations of motion, has the right non-relativistic reduction, and gives the correct Schödinger equation. It is the only Lagrangian that does all this and is quadratic in the velocities.
Getting the path integrals to actually converge took a bit of thought. The usual tricks with small factors of iε or Wick rotation don’t work: they cause the path integrals to blow up in either past or future, depending which sign you use.
However if we compute the path integrals on a wavelet by wavelet basis, they converge without any help. The Gaussians ensure convergence.
The normalization is given, up to a phase, by requiring unitarity:
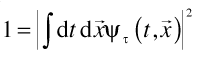
The expression for the path integrals is then:
![]()
![]()
We have actually one more thing to think about: how do we define the laboratory time in a way that is frame independent? If we use the proper time of the particle, we won’t be able to generalize this to the many particle case in any reasonable way. For a third time, Morlet wavelets come to the rescue. We again break up the wave function into its component wavelets; then compute the starting position and momentum for each wavelet:
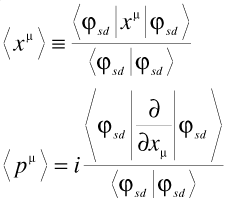
and use the geodesic time for that wavelet to the detector. The geodesic time is frame-invariant so we done (modulo some subtleties discussed in the paper). At the end of course we put Humpty-Dumpty back together again, constructing the final wave function as the sum over the results for each wavelet.
From the path integral to go one infinitesimal step in time forward we get the Schödinger equation:
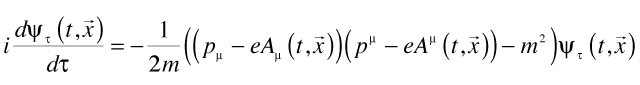
with the four momentum operator:
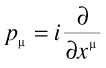
The stationary solutions of this are just the solutions of the Klein-Gordon equation, with the minimal substitution:
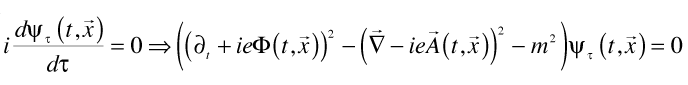
Since the electron mass is associated with a very high frequency:
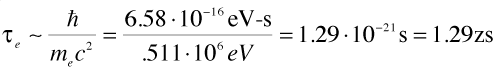
We recover the standard quantum theory as the low frequency limit of quantum mechanics: over times much longer than a zeptosecond, the effects of quantizing time are likely to be averaged out.
If we define the relative quantum time as the difference between the quantum time and the current laboratory time:
![]()
We can rewrite the Schödinger equation in a way which makes it easy to see the effects of small fluctuations in quantum time from the laboratory time:
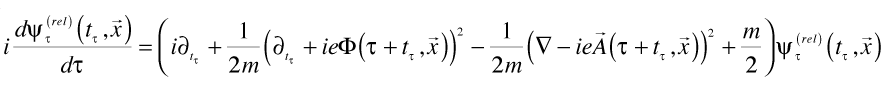
And as I discuss in the paper, taking the stationary state condition as defining the bound state energies lets us recover the Bohr orbital condition as well, so we get the usual bound states (plus a bit of fuzz in time).
In general, temporal quantization is to standard quantum mechanics (with respect to the time dimension) as standard quantum mechanics is to classical mechanics.
How to test?
There are now hundreds of foundational experiments in quantum mechanics. For most of them, flipping time and a space dimension gives a test of quantum time. I look at a few in the paper: single and double slit in time (of course), pre- and post-acceleration effects of time-varying fields, and the Aharonov-Bohm experiment in time.
The requirement of the most complete possible symmetry between time and space puts a strong constraint on quantum time: it has no free parameters. Therefore the experimental predictions are unambiguous. Further, it is difficult to see how, given relativity, it would be possible to have a wave function “flat” in time in one frame without being partly “fuzzy” in time in any frame connected to the first by a boost.
Whether temporal quantization is the correct way to model such fuzziness in time, it at least provides a well-defined way to analyze experiments looking for quantum effects along the time axis.
No Comments
No comments yet.
RSS feed for comments on this post. TrackBack URI
Leave a comment
You must be logged in to post a comment.