Next step for time & quantum mechanics
“When you come to a fork in the road, take it!” — Yogi Berra, Quantum Philosopher
I’ve been wondering what to do with quantum time. I’ve gotten a certain amount of feedback on the original paper, ranging from “hard but interesting” to “interesting but hard”.
There are really two directions I would like to take this project at this point:
- Do the calculations in a more transparent way, to leave us, hopefully, just with “interesting”.
- Extend the ideas to the multi-particle case, which is needed for the analysis of all but the most trivial cases. For instance, we need this even to compute bound state wave functions.
In the spirit of quantum mechanics, it seems best to do both. I look at each in turn.
I noticed when I talked in Baltimore last month that the animations were really the most transparent part of the talk. But the only way to develop them is to use numerical methods. I’ve done a bit of numerical work in the past, mostly to calculate charged particle orbits around a black hole (when I was a grad student at Princeton). From this I learned two things:
- Numerical calculations are tricky. I learned this the hard way. I had thought — ah youth — that the smaller you make the step size, the more accurate the results. But I found this was true only up to a point; below a certain step size the calculations would produce obvious nonsense: at small enough step sizes, round-off errors dominated the results, sending the particles either into the black hole or out into space. [No real particles were harmed in the course of this experiment.] Ultimately, I had to completely rewrite the equations in a non-linear but stabler way to get something meaningful.
- If you don’t have a reliable source of physical intuition, tricky can quickly escalate into nonsense. With anything involving time this is particularly a problem, largely because our usual intuition about time is so compelling that it is hard to move past it. And if we do move past it, where do we get a “reliable source of physical intuition”?
Consequently I’ve been a bit chary of doing numerical work. But while researching my Baltimore talk, I came across a work, Advanced Visual Quantum Mechanics, by Bernd Thaller, where the problem was solved, at least for low dimensional cases. Bernd Thaller worked primarily with Mathematica, a higher level language, but used a C program written by Manfred Liebmann for the low level numerical work. This was a dissertation paper by Liebmann. A quick scan of the table of contents was enough to confirm my intuition that the problem is non-trivial.
I’ve spent a few hours with Liebmann’s dissertation. It is written in German but apparently my high school German, Google translate, and a fair knowledge of the subject area [plus checking the references as I go] is enough to let me stumble thru it. The basic approach is essentially path integrals done a step at a time, in such wise as to minimize the numerical error at each step. This I can manage. Approximate proudly!
The second problem is how to extend quantum time to the multi-particle case. The main problem here is how to generalize the single particle results to the multi. After some mulling, and in the spirit of “approximate proudly” I’ve decided that using the usual Feynman rules but with the standard propagator replaced by the slightly fuzzier quantum time propagator is a reasonable first step. When we are only looking for first order corrections, we don’t need an elaborate theoretical framework.
What to use for the “slightly fuzzier” is a bit of a question. Our single particle action is:

The most obvious generalization to the field theoretical case looks like:
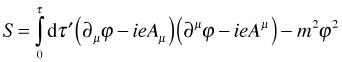
This won’t do. It is dimensionally wrong. We need to multiply τ by something with dimensions of mass. But we can’t use the mass of any specific particle, as that would be to prefer one over another. We will instead insert a factor κ, defined as something with dimensions of mass/energy:
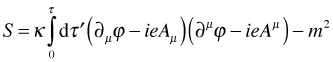
This will give us [insert hand-waving here] a propagator looking like:
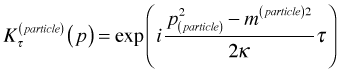
If we are looking at a Feynman diagram we will wind up convoluting over the laboratory time:

Which makes most of our integrals look like products of the Laplace transform of the propagator:
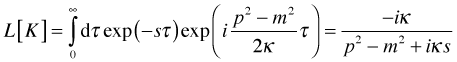
Compare to the usual Feynman propagator:
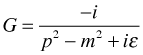
Modulo an overall dimensional factor of κ [the sort of thing that comes out in the wash], they look much alike — in the limit of small κ. As small κ corresponds loosely to large τ and as we expect to get standard quantum theory back in the long time limit of quantum time, this is fine.
The next question is where did κ come from? We don’t need to sort that out entirely up front, but we do need to know we have at least one viable answer.
If we want to take an aggressively Machian view of quantum mechanics, then there is nothing to the universe but its wave function: space and time are mere ensemble averages over the wave function of the rest of the universe. κ then can be a measure of how much energy stored in the local vacuum fluctuations, small but not zero:
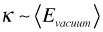
So, that is the plan for the multi-particle case: use the κ-ified propagator with the Feynman rules, require we get standard quantum theory back in the large τ/small κ limit, see the testable inferences in re quantum time/multiple particle case as the first order corrections due to non-zero κ and/or small dispersions along the time dimension.